
Hvordan påvirker bedriftens størrelse predikering av konkurs? (F)
Hvilke variabler påvirker modeller som brukes for å forutse en konkurs? I denne studien undersøkes det om størrelse er en viktig parameter. Forskerne finner at flere modeller er mindre nøyaktige for de minste og største selskapene, noe som innebærer at de utvikles spesifikt for visse størrelsesutvalg dersom man ønsker bedre prediksjoner.
Sammendrag

Ibrahim Pelja er siviløkonom fra Norges Handelshøyskole (NHH), hvor han for tiden er ph.d.-stipendiat som forsker på kredittrisiko.

Ranik Raaen Wahlstrøm er førsteamanuensis ved NTNU Handelshøyskolen og har doktorgrad fra samme institusjon. Hans forskning omfatter tema som finans, økonomistyring, regnskap, datavitenskap, statistikk og maskinlæring. Han har også jobbet flere år i privat næringsliv, bl.a. som økonomisjef, autorisert regnskapsfører, styremedlem og forretningsutvikler.
Sannsynligheten for konkurs er av interesse for flere aktører. Mange forsøker derfor å unngå eller redusere fremtidige tap ved å predikere konkurs ved hjelp av statistiske modeller. Det er derfor viktig å forstå hvilke faktorer som kan påvirke disse konkursmodellene. I denne studien undersøker vi hvorvidt bedriftens størrelse har betydning ved predikering av konkurs. Våre funn viser at prediksjonsmodellene vi tester, er mindre nøyaktige for de minste og største selskapene. Implikasjonene av dette er at konkursprediksjonsmodeller må utvikles spesifikt for visse størrelsesutvalg hvis man ønsker bedre prediksjoner, på lik linje med tidligere forskning som har funnet lignende for bransjer.
Introduksjon
Konkurs gir betydelige negative konsekvenser, slik som tap av egenkapital, utlån, arbeidsplasser og fremtidige skatteinntekter. Mange aktører er derfor interessert i å anslå hvilke bedrifter som er i fare for å gå konkurs, slik at man kan gripe inn på et tidlig tidspunkt for å redde bedriften eller redusere de negative konsekvensene. I lys av dette er det ikke overraskende at flere aktører anvender statistiske modeller for å predikere konkurs i selskaper.
Vi undersøker i denne studien hvordan prediksjonsevnen til disse modellene varierer med størrelsen på bedriftene de benyttes på. Vår undersøkelse er dels motivert av tidligere studier som finner at regnskapsinformasjon er dårligere til å predikere fremtidig lønnsomhet hos mindre bedrifter (Bathke et al., 1989; Dichev & Tang, 2009). Dette problematiseres ytterligere av Beaver et al. (2005), som fant at regnskapet over tid har blitt mindre egnet til å predikere konkurs. Tapet i prediksjonsevne kan kompenseres for ved å anvende markedsinformasjon, men dette er kun tilgjengelig for et fåtall bedrifter. Videre er vår hypotese motivert av Chava og Jarrow (2004), som viste at bransjeforskjeller påvirker modeller for konkursprediksjon. Vi forventer at det samme er tilfellet for bedrifter av forskjellig størrelse.
Det er ikke nødvendigvis innlysende hvordan prediksjonsevnen varierer med bedriftsstørrelse. På den ene siden kan det virke åpenbart at det er vanskeligere å komme med prediksjoner for små bedrifter, blant annet fordi regnskapskvaliteten er antatt dårligere og inntjeningen mer volatil (Dichev & Tang, 2009). På den andre siden vil større bedrifter ofte være mer komplekse, og det kan derfor være vanskeligere å predikere konkurs hos disse ved hjelp av en håndfull nøkkeltall fra regnskapet. For større bedrifter kan det for eksempel være mer aktuelt å vurdere mulighetene for å hente ny kapital, selge deler av driften eller gjennomføre sammenslåinger eller oppkjøp.
Resultatene våre viser at modellenes evne til å predikere konkurs varierer med størrelsen på bedriftene. Modellenes prediksjonsevne er dårligere for de minste bedriftene, men stiger med bedrifters størrelse helt til et toppunkt for bedrifter med eiendeler på rundt 5–10 millioner, før prediksjonsevnen faller igjen med økende størrelse. Grunnlaget for analysen er årsregnskaper fra norske aksjeselskaper i perioden 2006–2014, og resultatene er robuste på tvers av ulike metoder og variabelsett. Våre funn har flere implikasjoner, hvorav den viktigste er behovet for størrelsesspesifikke modeller for konkursprediksjon.
Relevant litteratur
Den banebrytende studien til Beaver (1966) viste at individuelle nøkkeltall kan predikere konkurs, noe som motiverte for ytterligere forskning på konkursprediksjon. Siden den gang er det publisert mange studier som samlet har utviklet utallige modeller for predikering av konkurs (Bellovary et al., 2007; Kumar & Ravi, 2007). Av disse studiene er det nødvendig å trekke frem Altman (1968) som utviklet den velkjente Z-score-modellen, Ohlson (1980) som utviklet O-score-modellen med logistisk regresjon (LR), Zmijewski (1984) som tok opp viktige metodiske problemer, og Shumway (2001) som illustrerte fordelene ved å anvende hasardmodeller for konkursprediksjon. Ulike aktører anvender forskjellige modeller, og det er ofte behov for å konstruere spesialiserte modeller tilpasset det relevante utvalget.
Tidligere studier har benyttet til sammen hundrevis av forskjellige variabler for konkursprediksjon. Imidlertid finnes det ingen konsensus eller veiledende teori om hvilke variabler som skal benyttes (Beaver et al., 2011; Tian et al., 2015). De tidligste studiene anvendte primært regnskapsvariabler (f.eks. Altman, 1968; Ohlson, 1980; Zmijewski, 1984), mens variabler basert på markedstall også er inkludert i senere tid, blant annet for å kompensere for regnskapstallenes reduserte relevans (Beaver et al., 2005; Chava & Jarrow, 2004; Shumway, 2001; Tian et al., 2015). Noen studier har i tillegg inkludert eierskap- og ledelsesvariabler, som for eksempel størrelsen på styret eller karakteristikker ved ledelsen (Liang et al., 2016; Platt & Platt, 2012). Valg av variabler har typisk vært basert på statistisk signifikans, skjønnsmessig vurdering eller en kombinasjon.
Videre er det heller ingen konsensus rundt hvilken metode som er best egnet til å predikere konkurs. Tidligere studier benyttet primært lineær diskriminantanalyse og LR (Dimitras et al., 1996). Førstnevnte har blitt kritisert, ettersom den antar normaldistribusjon av variablene og lik varians-kovarians-matrise på tvers av klassene for det som skal predikeres (Joy & Tollefson, 1975). LR har derimot ikke like begrensende antakelser og gir i tillegg mer intuitive utgangsverdier (Ohlson, 1980). I senere tid har maskinlæringsmetoder blitt vanligere, hvorav nevrale nettverk (NN) har vært den mest brukte metoden (Bellovary et al., 2007; Kumar & Ravi, 2007). NN fanger et bredt spekter av relasjoner uten å gjøre antakelser om data eller residualer, og de har vist seg å gi bedre konkursprediksjoner sammenlignet med andre maskinlæringsmetoder (Zhang et al., 1999; Alaka et al., 2018). Dette er også bekreftet av Næss et al. (2017), som gjennomførte en empirisk sammenligning av forskjellige metoder og fant at modeller basert på generell LR og NN best predikerte konkurs i norske bedrifter.
Metode
Data og definisjon av konkurs
Innledningsvis besto datagrunnlaget av ikke-konsoliderte årsregnskaper fra alle norske ikke-børsnoterte aksjeselskaper i perioden 2006–2016 samt alle registrerte konkurser i perioden 2006–2017. Data ble levert av Brønnøysundregistrene. Vi fulgte Bernhardsen og Larsen (2007) og ekskluderte alle årsregnskaper med eiendeler mindre enn NOK 500 000. I samsvar med vanlig praksis i litteraturen ekskluderte vi alle årsregnskaper fra bedrifter innenfor bransjene finansiering og forsikring, omsetning og drift av fast eiendom, kraftforsyning og vann, avløp, renovasjon (Mansi et al., 2012). I tillegg ekskluderte vi alle årsregnskaper fra bedrifter hvor bransje ikke er rapportert, eller hvor bedriftens formål er kun investering (holdingselskaper).
Vi fulgte vanlig praksis i litteraturen ved å definere konkurs basert på dato for registrert konkurs (Gupta et al., 2018). Dette gjorde vi ved å anvende samme definisjon for konkurs som ved utviklingen av SEBRA-modellen, som er en modell utviklet av Norges Bank, og som brukes blant annet av Finanstilsynet (Bernhardsen & Larsen, 2007) Et årsregnskap definerte vi som et konkursregnskap dersom i) det var det siste årsregnskapet fra bedriften, og ii) bedriften registrerte seg, eller en domstol registrerer den, for konkurs innen tre år etter balansedatoen for årsregnskapet. Alle andre årsregnskaper definerte vi som ikke-konkursregnskaper. Blant bedriftene i datagrunnlaget observerte vi at 99,2 prosent, 85,9 prosent og 22,7 prosent ble registrert som konkurs innen henholdsvis tre, to og ett år etter siste leverte årsregnskap. Dette samsvarer med Theodossiou (1993) og Tinoco og Wilson (2013). På grunn av denne tidsforskjellen på tre år, og fordi vi hadde tilgjengelig registrerte konkurser til og med 2017, ekskluderte vi alle årsregnskaper etter 2014. Etter alle ekskluderinger nevnt ovenfor besto datasettet av 992 369 årsregnskaper mellom 2006 og 2014, hvorav 1,51 prosent er klassifisert som konkursregnskaper.
Balansering, estimering og evaluering
Zmijewski (1984) viste hvordan modeller for konkursprediksjon forvrenges dersom datasettet som benyttes for å utvikle dem, har et forhold mellom observasjoner av konkurs og ikke-konkurs som avviker fra den virkelige populasjonen. Imidlertid er det relativt få bedrifter som går konkurs. Dette vil skape et klassebalanseproblem dersom vi benytter alle tilgjengelige data, noe som sannsynligvis også vil forvrenge modellene (Liang et al., 2016). Vi fulgte derfor vanlig praksis ved å balansere datasettet slik at det består av like mange konkursregnskaper som ikke-konkursregnskaper. En slik tilnærming ble støttet av Li og Sun (2012), som fant at konkursprediksjon blir bedre med et balansert datasett. Videre tilskriver en slik tilnærming mer vekt til konkursregnskaper siden deres andel i datasettet blir relativt større. Dette er fordelaktig ettersom det er mer kostbart å predikerte et konkursregnskap feil (Altman et al., 1977).
For å oppnå et balansert datasett valgte vi ikke-konkursregnskaper som samsvarte godt med konkursregnskaper langs tre av de vanligste dimensjonene – størrelse, bransje og regnskapsår (Appiah et al., 2015). Først inkluderte vi alle konkursregnskaper. Deretter inkluderte vi for hvert av disse det ikke-konkursregnskapet med minst forskjell i størrelse (målt etter eiendeler) blant dem innenfor samme bransje og samme regnskapsår. Ingen regnskaper ble inkludert flere ganger. Videre fulgte vi litteraturen og begrenset verdiene av variablene mellom 1. og 99. prosentil innenfor hvert regnskapsår (Shumway, 2001; Tian et al., 2015).
Alle modeller ble estimert og evaluert seks ganger, som illustrert i figur 1. For hver gang prediksjonsevnen til modellene evaluert på et testsett bestående av alle årsregnskaper i det balanserte datasettet for ett av regnskapsårene 2009–2014. Videre ble modellene estimert for hver av disse gangene med et estimeringssett bestående av alle årsregnskapene i det balanserte datasettet for de tre foregående regnskapsårene.
Figur 1.
Illustrasjon av estimerings- og evalueringsprosessen.
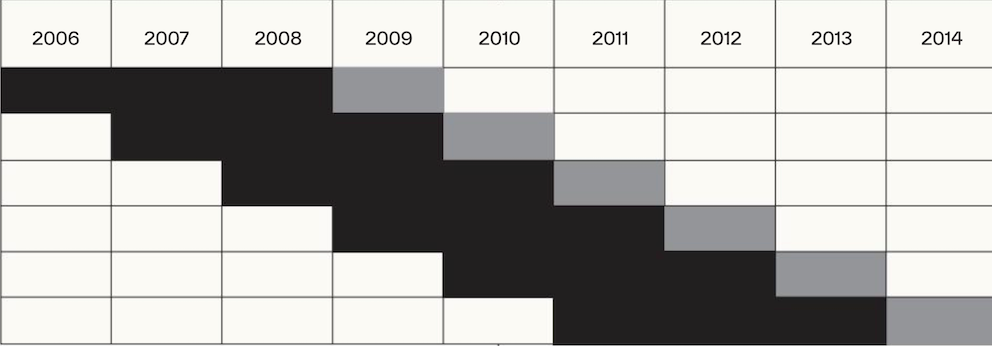
Alle modeller estimeres og evalueres seks ganger. For hver gang evalueres prediksjonsevnen til modellene på et testsett bestående av alle årsregnskaper i det balanserte datasettet for ett av regnskapsårene 2009–2014 (lysegrått). Videre estimeres modellene for hver av disse gangene med et estimeringssett bestående av alle årsregnskapene i det balanserte datasettet for de tre foregående regnskapsårene (mørkegrått).
Prediksjonsevnen på testsettene ble evaluert basert på nøyaktighetsratio (NR)[1]. Dette målet er mye benyttet i litteraturen og er bedre enn antall korrekt klassifiserte ettersom det tar hensyn til både feilkostnader og skjevheter i datasettet (Huang & Ling, 2005). NR har en verdi mellom 0 og 1, hvorav 0 tilsvarer tilfeldig prognose og 1 tilsvarer perfekt forklaringskraft. NR mellom 0,4 og 0,6 er ansett som akseptabelt, mens NR over 0,6 er ansett som utmerket (Hosmer et al., 2013). I tillegg evaluerte vi basert på desilrangering, noe som også er mye benyttet i litteraturen (Tian et al., 2015). Dette vil si at vi først lot modellene predikere, for hvert årsregnskap i testsettet, en sannsynlighet for at det er et konkursregnskap. Deretter sorterte vi alle årsregnskaper inn i desiler basert på denne predikerte sannsynligheten. Årsregnskaper i første desil ble dermed de 10 prosentene av årsregnskapene som det ifølge modellen var høyest sannsynlighet for var konkursregnskaper, og så videre. Til slutt rapporterte vi andelen av alle årsregnskaper som faktisk ble definert som konkurs i hver desil. Flere faktiske konkursregnskaper i de første desilene, og følgelig færre faktiske konkursregnskaper i de siste desilene, indikerer en bedre prediksjonsmodell.
Størrelsesutvalg
For å undersøke effekten av bedrifters størrelse delte vi alle årsregnskaper inn i ni utvalg basert på størrelse målt i eiendeler. Tabell 1 viser grenseverdiene for størrelsesutvalgene samt antall årsregnskaper innenfor hvert evaluerings- og testsett for hvert regnskapsår og størrelsesutvalg. Estimering og evaluering, som angitt ovenfor, ble gjennomført innenfor hvert av disse ni størrelsesutvalgene. Vi brukte egengenererte grenser for størrelsesutvalgene for å oppnå tilstrekkelig med årsregnskaper i hvert utvalg. Desilinndeling ble ikke benyttet fordi dette gir for lite spredning i størrelse på tvers av utvalgene, ettersom det er stor overvekt av små bedrifter i populasjonen.
Tabell 1.
Deskriptiv statistikk for det endelige datasettet.
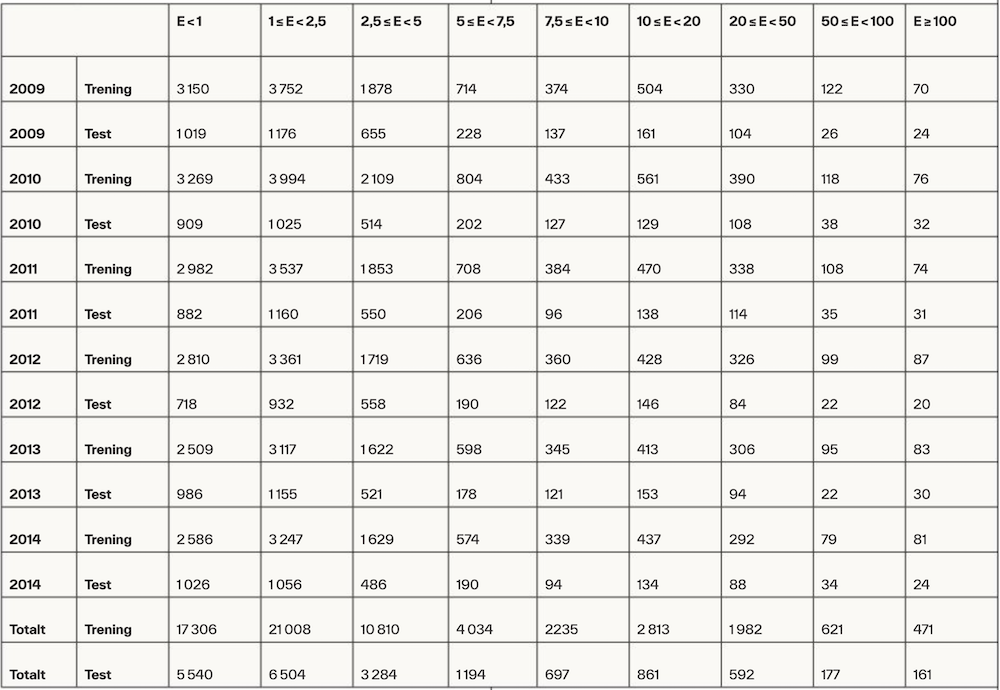
Tabellen viser antall årsregnskaper i det balanserte datasettet innenfor størrelsesutvalgene basert på eiendeler i millioner NOK (E) og innenfor hvert trenings- og testsett for hvert av de regnskapsårene hvor vi estimerer og evaluerer modeller (2009–2014). Testsettet inneholder alle årsregnskaper fra det aktuelle regnskapsåret som evalueres, mens estimeringssettet er årsregnskaper fra de tre foregående regnskapsårene (se figur 1).
Variabler
Vi benyttet tre relevante variabelsett fra tidligere studier, som angitt i tabell 2. Det første variabelsettet er de konvensjonelle nøkkeltallene som benyttes i modellen utviklet av Altman (1968). Denne modellen er mye anvendt av både praktikere og akademikere (Appiah et al., 2015; Tian et al., 2015), og det er vist at den predikerer tilstrekkelig godt også på norske data (Aae et al., 2018). Det andre variabelsettet er hentet fra Altman og Sabato (2007) og er utviklet spesifikt for små og mellomstore bedrifter. Det tredje variabelsettet er hentet fra SEBRA-modellen (Bernhardsen & Larsen, 2007).
Tabell 2.
Nøkkeltall i de tre utvalgte variabelsettene.
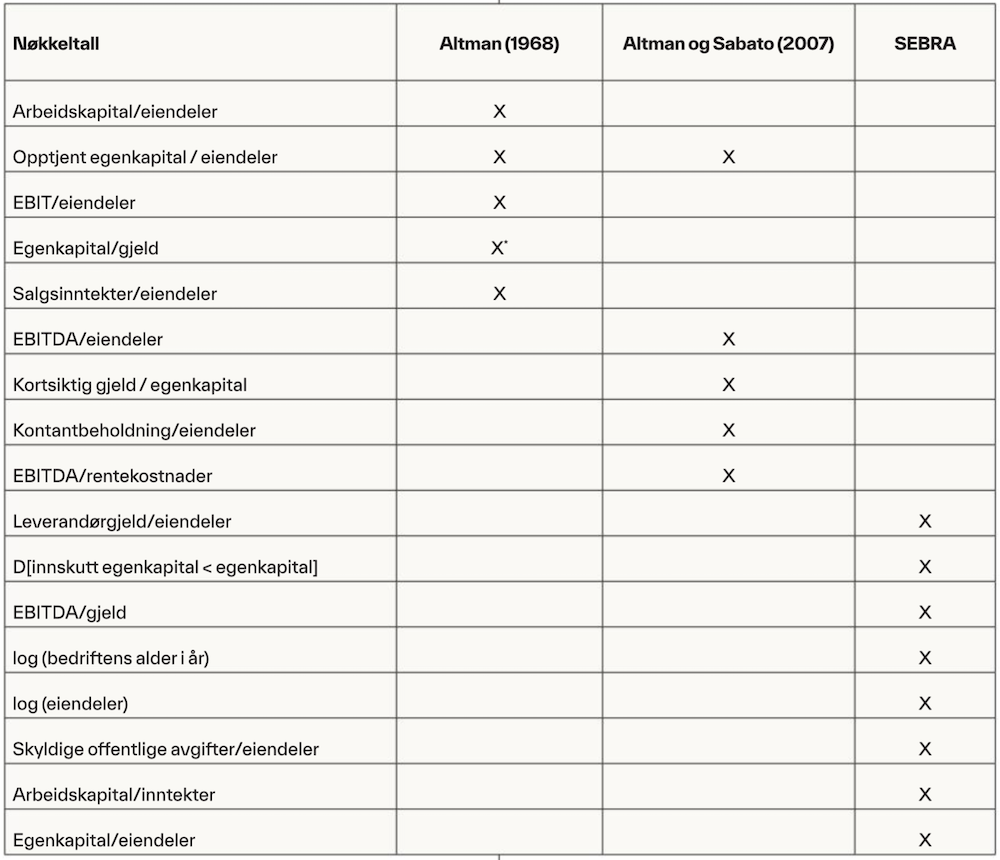
Tabellen viser de tre variabelsettene som benyttes. Et kryss i de ulike kolonnene indikerer at nøkkeltallet er inkludert i det respektive variabelsettet. Variabelen D [innskutt egenkapital < egenkapital] er en dummyvariabel med verdien 1 dersom egenkapital er større enn innskutt egenkapital. EBIT = resultat før renter og skatt. EBITDA = resultat før renter, skatt, avskrivninger og nedskrivninger. Altman (1968) bruker originalt markedsverdien av egenkapital. Vi bruker bokført verdi i samsvar med Altman (1993) for å tilpasse modellen for ikke-børsnoterte bedrifter.
Estimeringsmetode
Vi anvendte både LR og et NN for å utlede modeller for predikering av konkurs. LR gir en vektor ![]() med predikerte sannsynligheter for konkurs gitt ved
med predikerte sannsynligheter for konkurs gitt ved ![]() hvor X=
hvor X= ![]() er verdiene av variablene i for årsregnskapene n,
er verdiene av variablene i for årsregnskapene n, ![]() og
og ![]() er koeffisienter, l er en vektor med størrelse Nx1 bestående av kun verdien 1, mens ⊘ angir Hadamard-divisjon (elementvis matrisedivisjon). Koeffisientene estimeres ved å minimere den negative verdien av den naturlige logaritmen av sannsynlighetsfunksjonen:
er koeffisienter, l er en vektor med størrelse Nx1 bestående av kun verdien 1, mens ⊘ angir Hadamard-divisjon (elementvis matrisedivisjon). Koeffisientene estimeres ved å minimere den negative verdien av den naturlige logaritmen av sannsynlighetsfunksjonen:
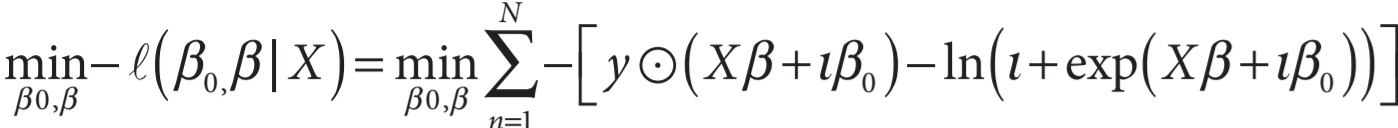
hvor y=![]() angir hvorvidt årsregnskapene n er klassifisert som faktisk konkurs (1) eller ikke konkurs (0), mens ⊙ angir Hadamard-multiplikasjon (elementvis matrisemultiplikasjon).
angir hvorvidt årsregnskapene n er klassifisert som faktisk konkurs (1) eller ikke konkurs (0), mens ⊙ angir Hadamard-multiplikasjon (elementvis matrisemultiplikasjon).
Videre benyttet vi et forovermatet NN, som illustrert øverst i figur 2. Dette har ett inngangslag, tre skjulte lag og ett utgangslag. Inngangslaget består av verdiene av variablene i. De skjulte lagene består av 20 noder hver, mens utgangslaget består av én node. Node m for lag L får en verdi for årsregnskap n basert på beregningen, som illustrert nederst i figur 2. Nodens inngangsverdier er verdiene av alle noder (eller variabler) fra det forrige laget. Disse multipliseres med hver sin vekt. Deretter benyttes summen av disse produktene og en biasverdi som inngangsverdi i en overføringsfunksjon. Alle vektene og biasverdiene er unike for hver node. Den siste noden representerer modellens prediksjon og vil følgelig få en verdi på mellom 0 (ikke-konkurs) og 1 (konkurs). Vi benyttet en lineær overføringsfunksjon for beregning av siste node , mens vi for alle andre noder benyttet en logaritmisk overføringsfunksjon[2]. NN-et ble estimert ved at alle vektene og bias verdiene ble tilpasset slik at siste node passet best mulig med observert konkurs (1) og ikke-konkurs (0) blant alle årsregnskapene i estimeringssettet.
Figur 2.
Illustrasjon av forovermatet nevralt nettverk.
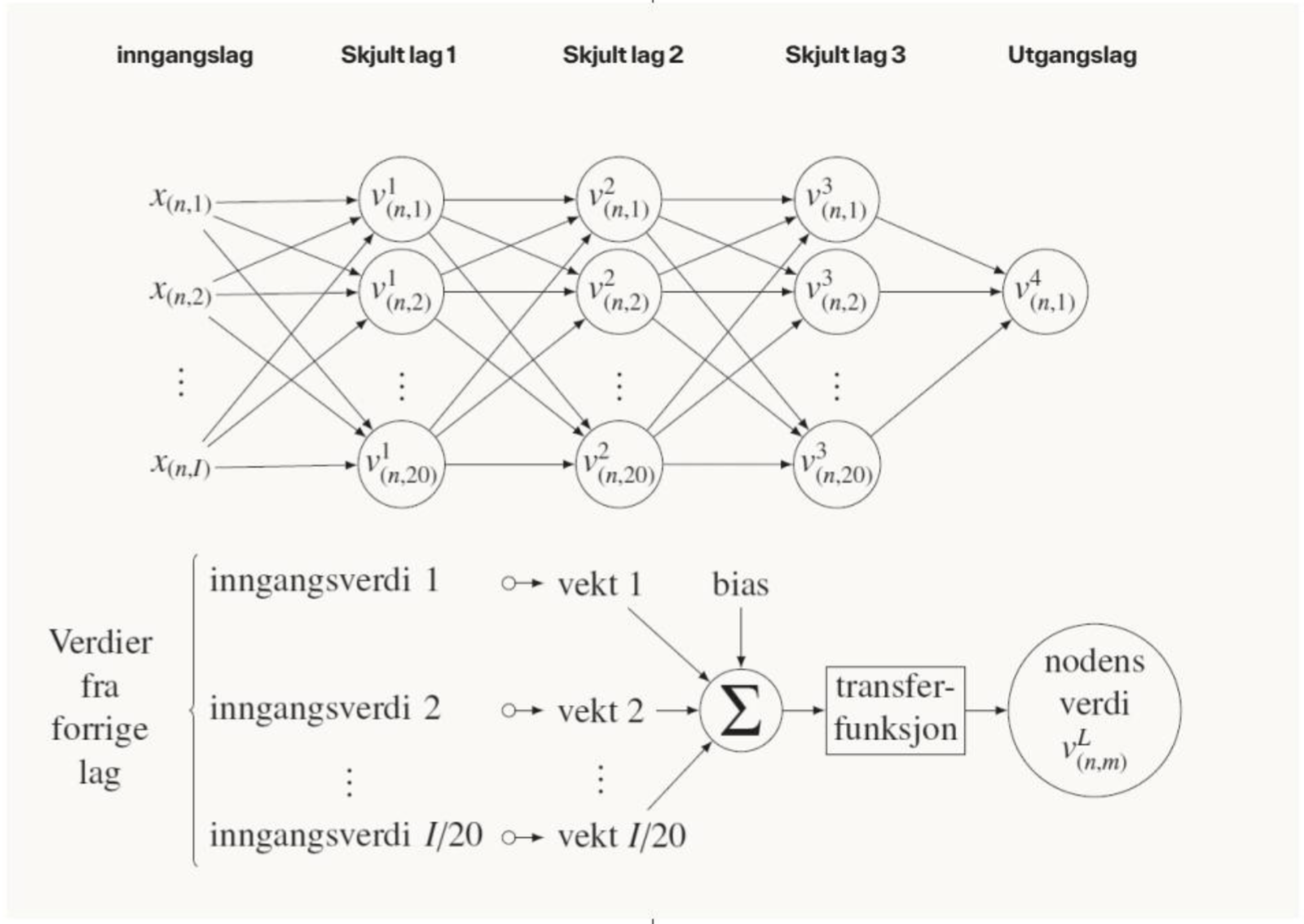
Øverst: Illustrasjon av det nevrale nettverket (NN-et) benyttet i vår studie, med angivelse av verdier for modellvariabler xn,I og noder for årsregnskap n. Nederst: Illustrasjon av verdiberegningen for hver node.
Resultater
For å forsikre oss om at resultatene er robuste på tvers av metoder og variabler, anvendte vi seks ulike modeller. Disse ble konstruert ved å kombinere de tre variabelsettene (tabell 2) og de to metodene (LR og NN). Figur 3 viser NR ved evaluering på testsettet for hvert regnskapsår (kryss) og gjennomsnitt på tvers av alle regnskapsårene (punkt) for hvert størrelsesutvalg. De seks panelene i figur 3 viser resultatene av analysen for hver av de seks modellene. Paneler til venstre (høyre) viser resultater for modeller utledet med LR (NN). Øverste, midterste og nederste paneler viser resultater for modeller med variabelsettet fra henholdsvis SEBRA-modellen, Altman (1968) og Altman og Sabato (2007). Det kommer frem at NR er lavere for både de minste og største bedriftene. Dette funnet er robust på tvers av de seks ulike modellene og indikerer at modeller for konkursprediksjon er dårligere tilpasset disse bedriftene. Vi legger også merke til at variasjonen i NR på tvers av regnskapsårene er større for de største bedriftene, men dette kan delvis skyldes mindre datagrunnlag.
I ikke-rapporterte resultater undersøkte vi om funnene skyldtes modellenes evne til å predikere konkursregnskaper eller deres evne til å predikere ikke-konkursregnskaper[3]. Vi benyttet da modellene slik de var estimert for figur 3, og undersøkte de predikerte sannsynlighetene for konkurs basert på modellene for alle årsregnskapene innenfor hvert størrelsesutvalg. For konkursregnskaper observerte vi at modellene predikerte lavere sannsynlighet for konkurs for de minste og største bedriftene sammenlignet med dem midt imellom. For ikke-konkursregnskaper observerte vi at modellene predikerte høyere sannsynlighet for konkurs for de minste og største bedriftene. Funnene i figur 3 er dermed et resultat av modellenes evne til å predikere konkurs for både bedrifter som faktisk gikk konkurs, og bedrifter som faktisk ikke gikk konkurs.
Figur 3.
NR ved evaluering på testsettet for ulike størrelsesutvalg.
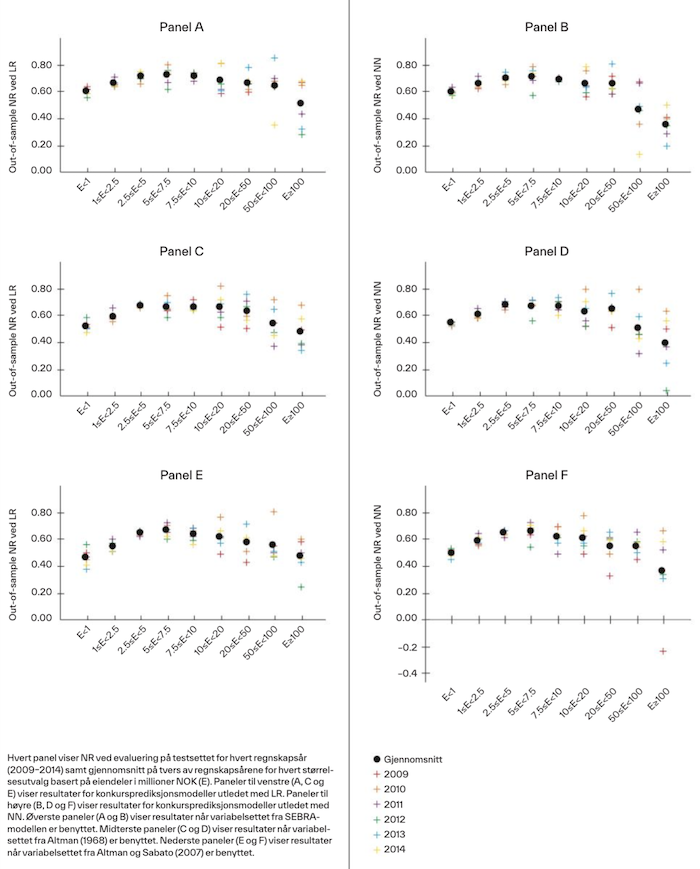
Tabell 3 viser desilrangeringer, altså andel konkursregnskaper innenfor hvert desil, hvor årsregnskaper sorteres inn i desiler basert på predikerte sannsynligheter gitt av modellene. Desil 1 inneholder de årsregnskapene hvor modellene har predikert høyest sannsynlighet for konkurs, og desil 10 inneholder de årsregnskapene som modellene har predikert å ha lavest sannsynlighet for konkurs. Andelene i tabell 3 vises for hvert størrelsesutvalg og er gjennomsnittet på tvers av alle modeller og regnskapsår (2009–2014). Gode modeller gir høyere andel for de laveste desilene og lavere andel for de høyeste desilene. Tabell 3 viser at dette er tilfellet for alle størrelsesutvalg. Videre er det generelt små forskjeller i desilrangeringene for de ulike størrelsesutvalgene, men vi legger allikevel merke til at det for de to største størrelsesutvalgene er lavere andel i desil 1 og 2 og høyere andel i desil 9 og 10 sammenlignet med de andre størrelsesutvalgene. Dette antyder at prediksjonene er dårligere for de største bedriftene sammenlignet med resten.
Tabell 3.
Desilrangeringer for ulike størrelsesutvalg (alle modeller og år).
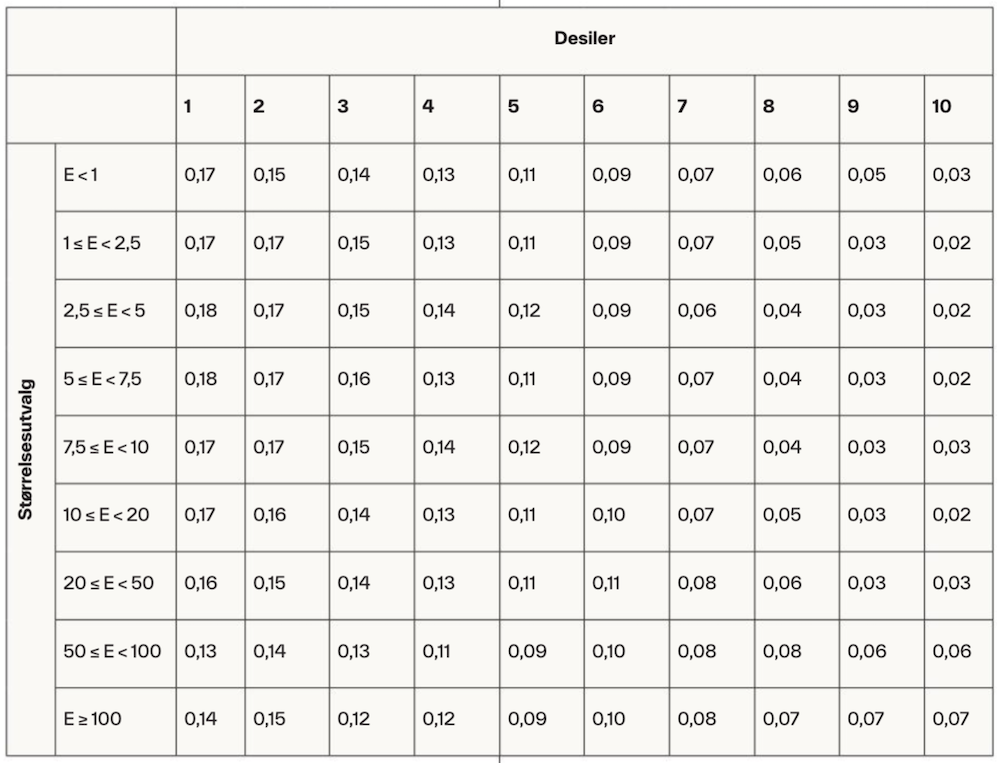
Tabellen viser andel av alle årsregnskaper definert som konkurs innenfor hvert desil (kolonner) for hvert størrelsesutvalg basert på eiendeler i millioner NOK (E). Årsregnskaper sorteres i desiler basert på predikert sannsynlighet for konkurs. Desil 1 inneholder de årsregnskapene hvor modellene har predikert høyest sannsynlighet for konkurs, og desil 10 inneholder de årsregnskapene hvor modellene har predikert lavest sannsynlighet for konkurs. Andelene er gjennomsnittlig andel på tvers av alle seks modeller og alle regnskapsårene.
Drøfting og implikasjoner
Den viktigste implikasjonen av våre funn er at det trolig må utvikles modeller tilpasset størrelsen på bedriftene de skal anvendes på. Dette kan for eksempel bety at modeller for konkursprediksjon bør benytte ulike variabler avhengig av størrelsen på bedriftene man skal predikere konkurs for. Dette er relevant for investorer, kreditorer og offentlige etater, inklusive Finanstilsynet, som anvender SEBRA-modellen for konkursprediksjon. Videre er en implikasjon av funnene at det kan være mindre attraktivt å innvilge kreditt til små bedrifter, siden modeller er dårligere til å predikere konkurs for disse. Dette er i så fall problematisk siden små bedrifter allerede har mindre tilgang på formell kapital. I tilfeller hvor små bedrifter likevel får kreditt, kan dette være til dårligere vilkår siden dårligere beslutningsgrunnlag betyr større risiko for kreditor. I sum kan dette begrense etableringsevnen og vekstmulighetene for mindre bedrifter. For større bedrifter understreker våre funn verdien av å inkludere andre informasjonskilder enn kun regnskapet ved konkursprediksjon, slik som markedsinformasjon eller nyheter som er mer tilgjengelige for større bedrifter. Til slutt underbygger våre funn at man bør vise varsomhet ved anvendelse av modeller for konkursprediksjon som ikke er utviklet spesifikt for de bedriftene man ønsker å benytte dem på.
Det er spesielt to faktorer som kan ha påvirket våre resultater. For det første observerer vi at det er stor forskjell i antall årsregnskaper i de forskjellige størrelsesutvalgene (se tabell 1). Dette kan påvirke modellenes prediksjonsevne ettersom treningsgrunnlaget er forskjellig. Vi ser dog at prediksjonsevnen ikke er høyest for de utvalgene som har flest årsregnskaper. For det andre må vi ta stilling til om resultatene kan være påvirket av eventuelle variasjoner i bransjesammensetning. Imidlertid observerer vi at fordelingen av bedrifter i de ulike bransjene er relativt konstant på tvers av størrelsesutvalgene. Dette er som forventet, siden vi som nevnt oppnår et balansert datasett ved å sammenligne konkursregnskaper og ikke-konkursregnskaper blant virksomheter innenfor samme bransje. Det er noe variasjon innen bransjene varehandel, overnattings- og serveringsvirksomhet, industri og bergverksdrift og utvinning. Endringene i bransjesammensetning utvikler seg dog lineært med størrelse og følger dermed ikke de ikke-lineære mønstrene vist i figur 3.
Vi håper vår studie kan brukes som grunnlag for fremtidig forskning på hva som kan være driverne for våre funn knyttet til prediksjonsevne og bedrifters størrelse. En slik innsikt kan være viktig for tiltak, slik som å lage spesifikke modeller for spesifikke bedriftsstørrelser. Det kan tenkes at en driver for våre funn er at det varierer med bedriftsstørrelse hvor godt regnskapene gjenspeiler virkeligheten. Nærliggende til dette forventer vi at større bedrifter presterer mer stabilt, og at dette kan bidra til variasjon i prediksjonsevne (Dichev & Tang, 2009). Videre kan modellenes evne til å predikere konkurs være avhengig av kompleksiteten innad i bedriftene, noe som ofte er et resultat av størrelsen på dem. Kompleksitet kan være driftsrelatert, slik som variasjon i produkter og produksjonsprosesser, og det kan være finansrelatert, slik som graden av forhandlingsmakt overfor kreditorer og tilgang på ytterligere ekstern kapital (Beck & Demirgüc-Kunt, 2006).
Oppsummert har vi vist i denne studien at de statistiske modellenes evne til å predikere konkurs varierer med størrelsen på bedriftene. De etablerte modellene vi testet, predikerer konkurs dårligere for de minste og største bedriftene. Disse funnene har viktige implikasjoner, hvorav vi spesielt trekker frem verdien av å utvikle modeller spesifikt for de bedriftene man skal benytte dem på. Fremtidig forskning bør undersøke hva variasjonen i prediksjonsevne skyldes, og hva som kan gjøres for å forbedre denne for de minste og største bedriftene.
Referanser
Alaka, H., Oyedele, L., Owolabi, H., Kumar, V., Ajayi, S., Akinade, O. & Bilal, M. (2018). Systematic review of bankruptcy prediction models: Towards a framework for tool selection. Expert Systems with Application, 94, 164–184.
Altman, E. I. (1968). Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance, 23(4), 589–609.
Altman, E. I. (1993). Corporate financial distress and bankruptcy: A complete guide to predicting & avoiding distress and profiting from bankruptcy (2. utg.). Wiley.
Altman, E. I. & Sabato, G. (2007). Modelling credit risk for SMEs: Evidence from the U.S. market. ABACUS, 43(3), 332–357.
Altman, E. I., Haldeman, R. G. & Narayanan, P. (1977). ZETA analysis: A new model to identify bankruptcy risk of corporations. Journal of Banking and Finance, 1(1), 29–54.
Appiah, K. O., Chizema, A. & Arthur, J. (2015). Predicting corporate failure: A systematic literature review of methodological issues. International Journal of Law and Management, 57(5), 461–485.
Bathke, A. W., Lorek, K. S. & Willinger, G. L. (1989). Firm-size and the predictive ability of quarterly earnings data. The Accounting Review, 64(1), 49–68.
Beaver, W. H. (1966). Financial ratios as predictors of failure. Journal of Accounting Research, 4, 71–111.
Beaver, W. H., Correia, M. & McNichols, M. F. (2011). Financial statement analysis and the prediction of financial distress. Foundations and Trends in Accounting, 5(2), 99–173.
Beaver, W. H., McNichols, M. F. & Rhie, J.-W. (2005). Have financial statements become less informative? Evidence from the ability of financial ratios to predict bankruptcy. Review of Accounting Studies, 10, 93–122.
Beck, T. & Demirgüc-Kunt, A. (2006). Small and medium-size enterprises: Access to finance as a growth constraint. Journal of Banking & Finance, 30(11), 2931–2943.
Bellovary, J. L., Giacomino, D. & Akers, M. D. (2007). A review of bankruptcy prediction studies: 1930 to present. Journal of Financial Education, 33, 1–42.
Bernhardsen, E. & Larsen, K. (2007). Modellering av kredittrisiko i foretakssektoren: Videreutvikling av SEBRA-modellen. Norges Bank.
Chava, S. & Jarrow, R. A. (2004). Bankruptcy prediction with industry effects. Review of Finance, 8(4), 537–569.
Dichev, I. D. & Tang, V. W. (2009). Earnings volatility and earnings predictability. Journal of Accounting and Economics, 47(1–2), 160–181.
Dimitras, A. I., Zanakis, S. H. & Zopounidis, C. (1996). A survey of business failures with an emphasis on prediction methods and industrial applications. European Journal of Operational Research, 90(3), 487–513.
Gupta, J., Gregoriou, A. & Ebrahimi, T. (2018). Empirical comparison of hazard models in predicting SMEs failure. Quantitative Finance, 18(3), 437–466.
Hosmer, D. W., Lemeshow, S. J. & Sturdivant, R. X. (2013). Applied logistic regression. John Wiley & Sons.
Huang, J. & Ling, C. X. (2005). Using AUC and accuracy in evaluating learning algorithms. IEEE Transactions on Knowledge and Data Engineering, 17(3), 299–310.
Joy, O. M. & Tollefson, J. O. (1975). On the financial applications of discriminant analysis. The Journal of Financial and Quantitative Analysis, 10(5), 723–739.
Kumar, P. R. & Ravi, V. (2007). Bankruptcy prediction in banks and firms via statistical and intelligent techniques: A review. European Journal of Operational Research, 180(1), 1–28.
Li, H. & Sun, J. (2012). Forecasting business failure: The use of nearest-neighbour support vectors and correcting imbalanced samples – Evidence from the Chinese hotel industry. Tourism Management, 33(3), 622–634.
Liang, D., Lu, C. C., Tsai, C. F. & Shih, G. A. (2016). Financial ratios and corporate governance indicators in bankruptcy prediction: A comprehensive study. European Journal of Operational Research, 252(2), 561–572.
Mansi, S. A., Maxwell, W. F. & Zhang, A. J. (2012). Bankruptcy prediction models and the cost of debt. The Journal of Fixed Income, 21(4), 25–42.
Næss, A. B., Wahlstrøm, R. R., Helland, F. F. & Kjærland, F. (2017). Konkursprediksjon for norske selskaper: En sammenligning av regresjonsmodeller og maskinlæringsteknikker. I T. Busch, J. O. Olaussen & I. J. Petterson (Red.), Bred og spiss! NTNU Handelshøyskolen 50 år: Et vitenskapelig jubileumsantologi (s. 313–330). Fagbokforlaget.
Ohlson, J. A. (1980). Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Reserch, 18(1), 109–131.
Platt, H. & Platt, M. (2012). Corporate board attributes and bankruptcy. Journal of Business Research, 65(8), 1139–1143.
Shumway, T. (2001). Forecasting bankruptcy more accurately: A simple hazard model. The Journal of Business, 74(1), 101–124.
Theodossiou, P. T. (1993). Predicting shifts in the mean of a multivariate time series process: An application in predicting business failures. Journal of American Statistical Association, 88(422), 441–449.
Tian, S., Yu, Y. & Guo, H. (2015). Variable selection and corporate bankruptcy forecasts. Journal of Banking & Finance, 52, 89–100.
Tinoco, M. H. & Wilson, N. (2013). Financial distress and bankruptcy prediction among listed companies using accounting, market and macroeconomic variables. International Review of Financial Analysis, 30, 394–419.
Zhang, G. Y., Hu, M. Y., Patuwo, B. E. & Indro, D. C. (1999). Artificial neural networks in bankruptcy prediction: General framework and cross-validation analysis. European Journal of Operational Research, 116(1), 16–32.
Zmijewski, M. E. (1984). Methodological issues related to the estimation of financial distress prediction models. Journal of Accounting Research, 22, 59–82.
Aae, E. L., Hansen, M. A., Pelja, I., Stemland, T. B. & Kinserdal, F. (2018). Er tradisjonelle regnskapsnøkkeltall relevante i en «moderne» IFRS-verden? Magma, 6, 52–62.
Noter
[1] NR er arealet under ROC-kurven (receiver operating characteristic curve) fratrukket 0,5 og multiplisert med 2 (Tian et al., 2015). ROC-kurven er en kurve hvor sann positivrate er plottet mot falsk positivrate for forskjellige grenseverdier for definisjon av hvilken klasse en predikert observasjon tilhører (Hosmer et al., 2013).
[2] Vi gjør oppmerksom på at LR i praksis er et forovermatet NN uten skjulte lag og med en logaritmisk overføringsfunksjon mellom inngangs- og utgangslaget.
[3] Alle ikke-rapporterte resultater vil bli gjort tilgjengelig ved forespørsel.
